پیش از درک مفهوم فوق بهتر است با یک مفهوم دیگر آشنا بشویم.
ماتریس تصادفی[1] چیست؟
ماتریسی تصادفی گفته میشود که دو شرط زیر را داشته باشد:
- مقادیر همه سلولها بزرگتر مساوی صفر باشد.
- جمع هر ستون برابر یک باشد.
به عنوان نمونه:
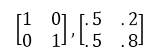
بر اساس تعریف فوق ماتریس همانی نیز یک ماتریس تصادفی است. همچنین هر ستون یک توزیع احتمال است.
هشتمین کارگاه آموزشی یادگیری عمیق (deep learning) (مجازی)
فرض کنید در یک شهر قاعدهای به صورت زیر وجود داشته باشد؛
- اگر امروز آفتابی باشد، فردا به احتمال 0.8 آفتابی است و اگر امروز ابری باشد فردا به احتمال 0.3 ابری است.
سوال این است که اگر امروز آفتابی باشد چقدر احتمال دارد که فردا ابری باشد؟
در این مساله احتمال یک نقطه از زمان (هر روز) تنها بستگی به وضعیت (روز) قبل دارد. چنین مسائلی را میتوان در قالب فرایند مارکف[2] مدلسازی کرد. در فرایند مارکف سلسلهای از آزمایشها (با مجموعه ثابتی از نتایج) با فواصل منظم روی داده و نتیجه آزمایش هر مرحله (وضعیت) تنها به وضعیت قبل بستگی دارد. در مثال فوق تنها کافی است وضعیت یک روز (آفتابی یا ابری) را بدانیم تا در مورد روزهای آتی بتوانیم نتیجهگیری کنیم.
ماتریس تحول اینجا خود را نشان میدهد. تنها چهار حالت داریم؛ دو حالت برای روز جاری و دو حالت برای روز بعد. این مقادیر را در یک ماتریس به صورتی قرار می دهیم که سطرها مقادیر آتی و ستونها مقایر جاری را در بر بگیرند.
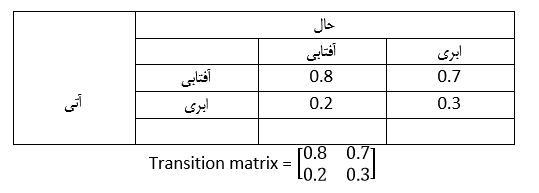
توجه داریم که هر ستون توزیع احتمال یکی از حالتهای وضعیت فعلی برای حالت آتی است. با در اختیار داشتن این ماتریس و مدلسازی وضعیت فعلی به صورت زیر:

بردار فوق نشان میدهد که روز فعلی آفتابی است. میتوان احتمال روز آتی را به صورت زیر محاسبه کرد:

بنابراین اگر امروز آفتابی باشد به احتمال 0.8 فردا آفتابی و به احتمال 0.2 فردا ابری است. سول بعدی این است که احتمال آفتابی بودن دو روز بعد چقدر است؟

توجه داریم که میتوان از توانهای مختلف ماتریس تحول برای انتقال به وضعیت مطلوب استفاده کرد.
یک مثال دیگر از کاربرد ماتریس تحول مدلسازی زبان با استفاده از unigram است. در این حالت احتمال کلمه آتی در متن تنها به کلمه قبل بستگی داشته و بنابراین میتوان از ماتریس تحول برای پیشبینی کلمه بعدی استفاده کرد.